What if literary appreciation could be approached through multifractal theory? We believe that it is possible. Let us explain how.
The perception of literary quality is an intriguing question that is almost impossible to answer completely. There are as many opinions about it as there are readers in the world. Even for one individual, the answer is not straight-forward. In one book, you might appreciate the aesthetics of the language, in another you might fall in love with the main character, while yet another novel takes you on an adventure to the other side of the world.
Every story, however, shares one characteristic: a narrative to follow. As the story unfolds, the narrative development reflects the emotional development of the plot. A compelling story resonates in the reader, evoking similar sentiments. As a feeler, the emotional development gets you engaged in the story.
What will happen next?
With recent advancements in sentiment analysis - how to computationally measure sentiments expressed in a text - it has become possible to capture the feelings in a story and to summarize the narrative structure in a sentiment arc.
However, the relation between literary appreciation and sentiment development is not that simple. We like tragedies. We like comedies. We get shocked if our favorite character dies. We get shocked if the villain stays alive. It seems that rather than being interested in the general trend of the sentiments, we are more captured by changes in it.
That’s why, instead of examining sentiment arcs as such, we at Fabula-NET are more interested in the dynamical structure and distribution of sentiments throughout a story.
By applying insights from multifractal theory to computational narratology, we develop novel methods to capture the variation and dynamic properties of the sentiments in a narrative.
Fractal theory meets literary theory
Fractals are complex patterns that are based on a simple underlying pattern which repeats itself at different scales. Fractality is everywhere: from blood vessels to tree branch structure, and from snow crystals to the structure of remote galaxis. So, why not in literature?
A simple literary fractal could be a sad story that in each chapter contains a smaller sad story. Every chapter begins a little more happily than how it ends. At the scale of the whole story, the overall sentiments also evolve from happy to sad. This is a fractal story.
Nevertheless, in the long run, this kind of self-repetitive structure would also become boring. The next chapter would never surprise the reader. That’s why we think that there exists a sweet spot of predictability and unpredictability in a good narrative. These dynamic properties can be modeled with a measure called the Hurst exponent. It approximates the inner coherence of the story arc. In short, a Hurst value under .5 would randomly oscillate around an average value. At around .5, the sentiment arc would exhibit some short-term correlations between emotional experiences, but it would still lack coherency at a longer scale. On the other hand, a Hurst value close to 1 would correspond to a story structure which is too monotonous and predictable.
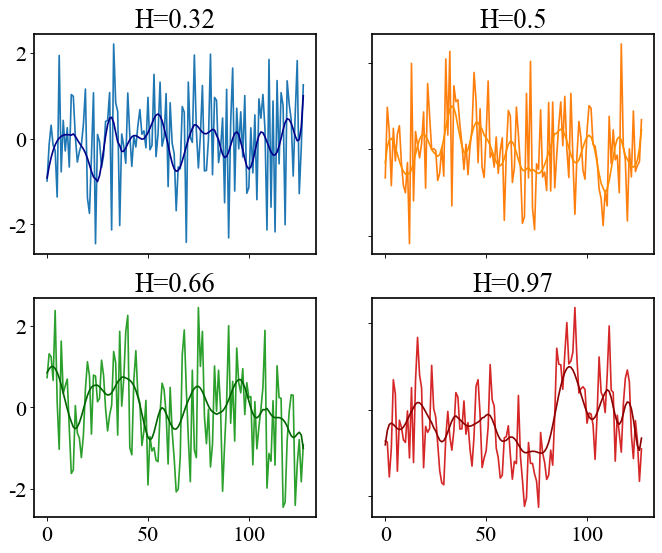
Examples of fractal time series with smoothed trend lines. As you can see, fractal series with lower Hurst values do not exhibit as clear patterns. When the Hurst exponent approaches 1, the nature of the time series becomes more rigid, which might be perceived as boring when applied to literature.
Indeed, the sweet spot we are looking for seems to exist somewhere in-between. Our first results support the hypothesis that an optimal Hurst value, around 0.55-0.65, contributes to the literary appreciation of a story.
Currently, we are at the beginning of a new story in the field of computational literary studies. In which other ways will Fabula-NET deepen our understanding of literature?