| Status: In Progress | First online: 27-05-2020 | Updated: 11-06-2020 |
Authors Kristoffer L. Nielbo Center for Humanities Computing Aarhus & Jianbo Gao, Beijing Normal University.
This study has not yet been peer reviewed.
Background
Newspapers provide high resolution data on public opinion. While they are neither unbiased or infallible, newspaper content reflects preferences, desires and values from all sides of the political spectrum. Particularly keyword-based methods (e.g., variation in ngram frequencies) have been used to study cultural dynamics in as diverse fields as consumer history [1], epidemiology [2], and linguistics [3]. Recently, we have seen a rise in more advanced applications of statistical learning to newspaper data sets model deep historically dynamics of word sense [4]. Interestingly, few, if any, studies try to reverse the inferential direction and use newspapers to predict future events and tendencies. In this paper, we develop a method for detecting change and modeling future trends from newspapers using techniques based information theory and fractal analysis. A previous version of the method has already been used to predict cultural trends in social media and discover bifurcations in influential authors’ creative development [5, 6]. The method is available as an open source library.
Methods
Initially, we linguistically normalize the newspaper articles and represent them as bag-of-words (BoW) model, using latent dirichlet allocation in order to generate a dense low-rank representation of each article. We then extract two related information signals from the temporally sorted BoW model: novelty as an article $s^{(j)}$’s reliable difference from past articles $s^{(j-1)}, s^{(j-2)} , \dots ,s^{(j-w)}$ in window $w$:
\begin{equation} \mathbb{N}_w (j) = \frac{1}{w} \sum_{d=1}^{w} JSD (s^{(j)} \mid s^{(j - d)}) \end{equation}
and resonance as the degree to which future articles $s^{(j+1)}, s^{(j+2)}, \dots , s^{(j+w)}$ conforms to article $s^{(j)}$’s novelty:
\begin{equation} \mathbb{R}_w (j) = \mathbb{N}_w (j) - \mathbb{T}_w (j) \end{equation}
where $\mathbb{T}$ is the transience of $s^{(j)}$:
\begin{equation} \mathbb{T}_w (j) = \frac{1}{w} \sum_{d=1}^{w} JSD (s^{(j)} \mid s^{(j + d)}) \end{equation}
These novelty-resonance model was originally propose in [7], but here we propose a symmetrized and smooth version by useing the Jensen–Shannon divergence ($JSD$):
\begin{equation} JSD (s^{(j)} \mid s^{(k)}) = \frac{1}{2} D (s^{(j)} \mid M) + \frac{1}{2} D (s^{(k)} \mid M) \end{equation}
with $M = \frac{1}{2} (s^{(j)} + s^{(k)})$ and $D$ is the Kullback-Leibler divergence:
\begin{equation} D (s^{(j)} \mid s^{(k)}) = \sum_{i = 1}^{K} s_i^{(j)} \times \log_2 \frac{s_i^{(j)}}{s_i^{(k)}} \end{equation}
To model trends, we apply a non-linear adaptive filter to the resonance signal due to the inherent noisiness of trend signals [8]. First, the signal is partitioned into segments (or windows) of length $w=2n+1$ points, where neighboring segments overlap by $n+1$. The time scale is $n+1$ points, which ensures symmetry. Then, for each segment, a polynomial of order $k$ is fitted. Note that $k=0$ means a piece-wise constant, and $k=1$ a linear fit. The fitted polynomial for $ith$ and $(i+1)th$ is denoted as $y^{(i)}(l_1 ),y^{(i+1)}(l_2 )$, where $l_1,l_2=1,2,. . .,2n+1$. Note the length of the last segment may be shorter than $w$. We use the following weights for the overlap of two segments.
\begin{equation} y^{(c)}(l_1 )=w_1y^{(i)}(l+n)+w_2y^{(i)}(l),l=1,2,. . .,n+1 \end{equation}
where $w_1=(1-\frac{l-1}{n}), w_2=1-w_1$ can be written as $(1-\frac{d_j}{n}),j=1,2$, where $d_j$ denotes the distance between the point of overlapping segments and the center of $ y^{(i)},y^{(i+1)} $. The weights decrease linearly with the distance between point and center of the segment. This ensures that the filter is continuous everywhere, which ensures that non-boundary points are smooth.
Finally, in order to describe the overall information state of the specific set of newspaper articles we fit resonance on novelty to estimate the $\mathbb{N}\times\mathbb{R}$ slope $\beta_1$:
\begin{equation} \mathbb{R}_i = \beta_0 + \beta_1 \mathbb{N}_i + \epsilon_i, ~~ i = 1, \dots, n. \end{equation}
Results
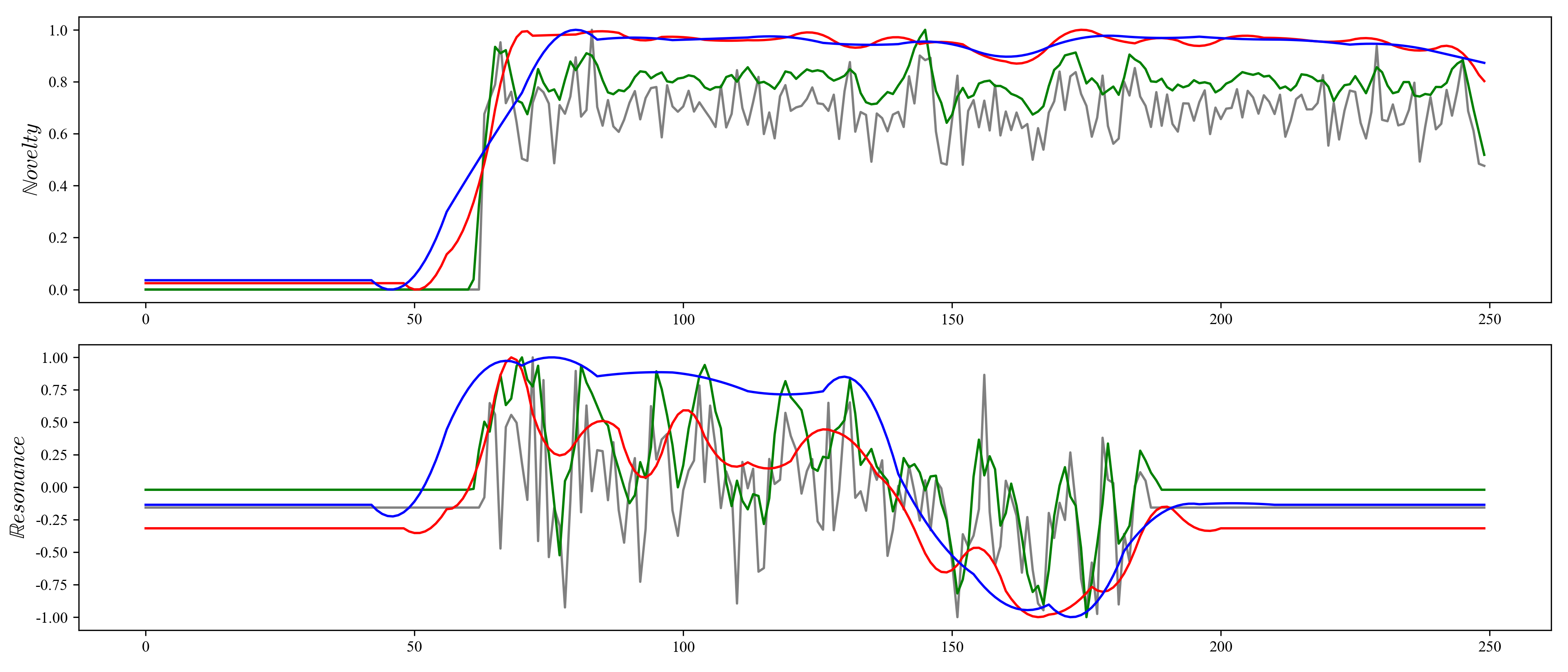Fig. 1: $\mathbb{N},\mathbb{R}$ estimated for Politiken over four days with a 1.5 day window.
Figure 1 depicts an information state of constant novelty, where every article introduces more or less novel content elements in comparison with 1.5 days of previous articles. This is the default state “hunger for novelty” state of news. A more troublesome trend can be observed from the resonance signal, because transience increases with time, and the news stories’ resonance decreases. This is a state of high uncertainty for the newspaper reader, where there is low persistence of news and the day-to-day experience is characterised by discontinuity. This can be further illustrated by figure 2, which indicates that there is only a weak realtionship between resonance and novelty ($\beta = 0.16 $). We propose to classify states of news as high uncertainty ($\beta < 0.5 $), neutral ($\beta \approx 0.5 $) and low uncertainty ($\beta > 0.5 $).
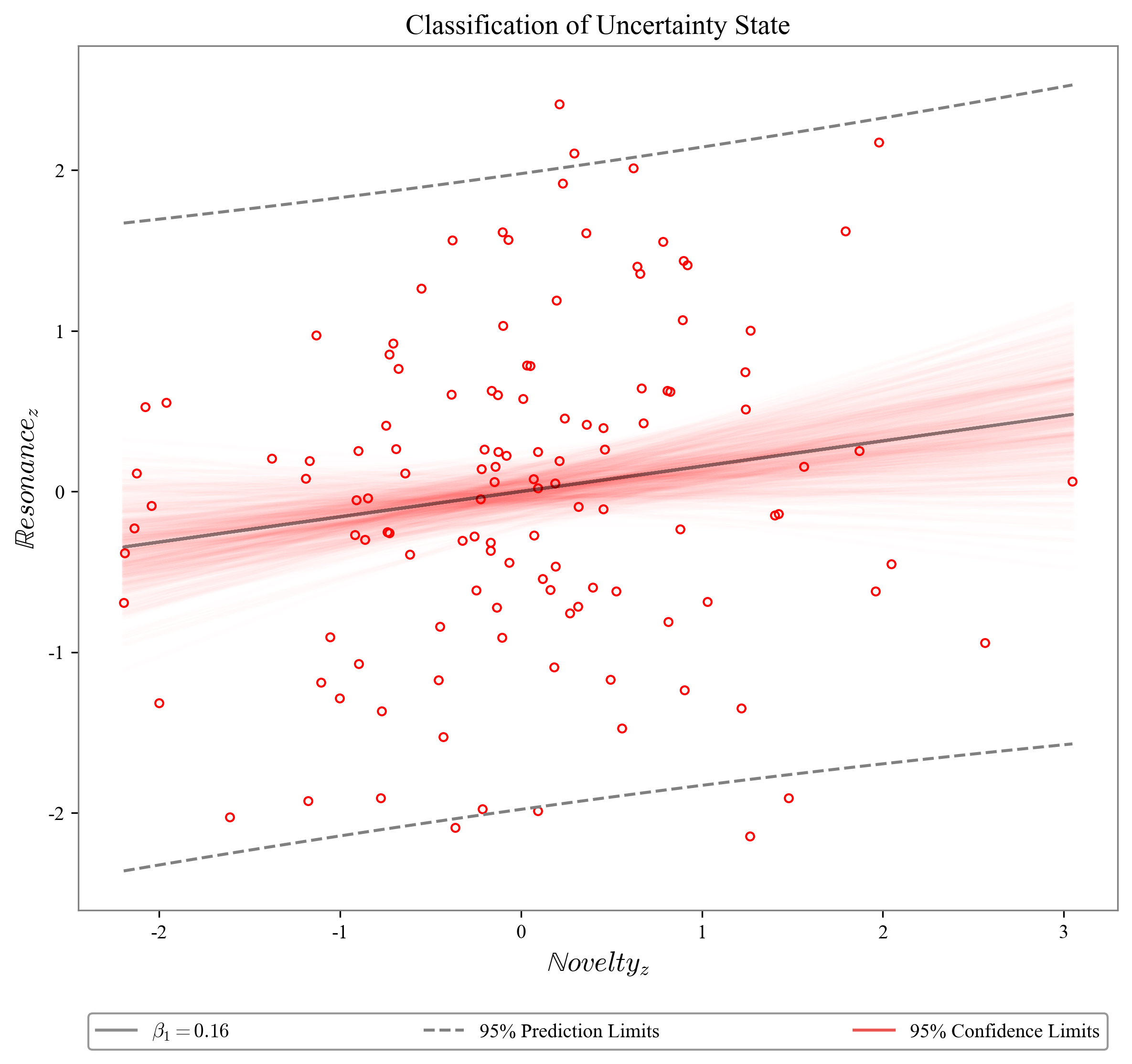Fig. 2: $\mathbb{N}\times\mathbb{R}$ slope of signals in fig 1 after normalization to zero mean. Confidence intervals are genereted using bootstrapping with 500 samples.
Resources
Comments submitted @ NDHL Website
Data available @ Contemporary newspaper data are proprietary. Please contact CHCAA for access to derived data.
Source code available @ CHCAA GitHub
Acknowledgment
This project is supported by the NeIC funded project Nordic Digital Humanities and the Carsberg funded project How Democracies Cope with COVID19 A Data-Driven Approach.
References
https://api.semanticscholar.org/CorpusID:51754560
1 M. Wevers, J. Gao, and K. L. Nielbo, “Tracking the Consumption Junction: Temporal Dependencies between Articles and Advertisements in Dutch Newspapers,” http://arxiv.org/abs/1903.11461 [cs].
2 Suppli, C.H., Hansen, N.D., Rasmussen, M. et al. (2018) Decline in HPV-vaccination uptake in Denmark – the association between HPV-related media coverage and HPV-vaccination. BMC Public Health 18, 1360.
3 Mikko, K., Dominowska, A., Hyttinen, E. et al (2017) “Big data approach to 19th-century Finnish newspaper literature,” https://api.semanticscholar.org/CorpusID:51754560
4 Tahmasebi, N. (2018) A Study on Word2Vec on a Historical Swedish Newspaper Corpus. Proceedings of the Digital Humanities in the Nordic Countries 3rd Conference.
5 Nielbo, K.L., Vahlstrup, P.B., Gao, J. & Bechmann A. (2020) Sociocultural trend signatures in minimal persistence and past novelty. Alliance of Digital Humanities Organizations 2020.
6 Vrangbæk E.E.H. & Nielbo, K. L. (accepted) Composition and Change in De Civitate Dei: A Case Study of Computationally Assisted Methods, Studia Patristica.
7 Barron, A. T. J., Huang, J., Spang, R. L., & DeDeo, S. (2018). Individuals, institutions, and innovation in the debates of the French Revolution. Proceedings of the National Academy of Sciences, 115(18), 4607–4612.
8 Gao, J., Hu, J., & Tung, W. (2011). Facilitating Joint Chaos and Fractal Analysis of Biosignals through Nonlinear Adaptive Filtering. PLoS ONE, 6(9), e24331.